А. А. Корнеев

http://kaa-07.narod.ru

ЛИМБИЧЕСКИЙ СПОСОБ ИССЛЕДОВАНИЯ

ЦИФРОВЫХ ОБЪЕКТОВ И СИСТЕМ

 

В этой статье будет рассмотрен вопрос об инструментарии исследователей, занимающихся изучением и анализом цифровых объектов и систем.

Один из самых простых и эффективных способов – это способ, который я назвал ЛИМБИЧЕСКИМ СПОСОБОМ отображения и преобразования.

 

Ниже, сначала на простых примерах, а затем при посредстве рассуждений и логики мы детальнее ознакомимся с указанным Способом.

 

Возьмём для начала простую задачку по изучению цифрового объекта, который представляет собой некий квадрат размером (3 х 3) с внутренней оцифровкой

(см. Рис. 1).

 

1	2	3
4	5	6
7	8	9

Рис.1

 

1. Пусть есть этот некий исходный квадрат со своей оцифровкой (см. Рис.1).
2. Пусть есть другой квадрат, где оцифровка иная (см. Рис.2)
3. Требуется найти графический способ для  отображения процесса перекодировки цифрового содержания таблиц (квадратов) из 1-го во 2-й.                                                                     

 

 

4	9	2
3	5	7
8	1	6

Рис.2

 

Способ перекодировки таблиц, их трансформации к другой оцифровке, в сущности, формально очевиден и прост – он сводится к тому, чтобы произвести замену одних цифр в одноимённых  и соответственных  клетках квадратов на другие цифры (числа) в другом квадрате.

 

Однако, хотя этот способ и очевиден, но он, к сожалению, совсем не нагляден.

 

Важное значение, имеет также конкретный порядок считывания  цифр  в квадратах, что на практике обычно не учитывается или считается, порой, мелочью…

 

В нашем, обучающем примере, взяты самые простые объекты (всего-то -  квадратная табличка размером - 3 х 3); но уже даже здесь возможны многочисленные варианты разного считывания  и отображения цифровых данных.

В частности, это могут быть:

• Построчное (слева – направо и сверху – вниз) считывание – ЗИГЗАГОМ
• Постолбцовое (сверху – вниз и слева – направо, по столбцам)
• И вообще, считывание по любой, заранее заданной траектории обхода, которая только может быть придумана и применена для исследования оцифровок обоих наших квадратов.

Ниже рассматривается простой способ отображения одной оцифровки в другую.

 

         Пусть порядок обхода (последовательность шагов обхода) исходного квадрата соответствует его внутренней оцифровке, т.е. последовательности цифр 1,2,3…до 9.

 

Итак:

Исходный квадрат. Горизонтальный обход зигзагом (№№ шагов обхода)	1	2	3	4	5	6	7	8	9
Итоговый квадрат	4	9	2	3	5	7	8	1	6

 

      Построим для графического отображения т.н. Лимб с 9 точками на окружности, через которые (от одной к другой) будем последовательно проводить линии, соответствующие шагам последовательного обхода объекта, - от одной цифры к другой. Это обход клеток квадратов будем вначале осуществлять ПО ГОРИЗОНТАЛЯМ нашего исходного объекта.

Тогда у нас лимб-9 для отображения получился такой:

 

 

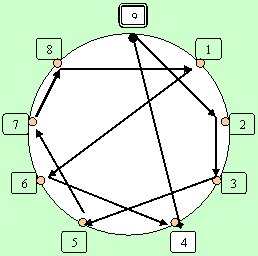
Рис.3

 

 

 

 

 

 

 

 

 

 

 

 

        А теперь попробуем совершить другой, уже  ВЕРТИКАЛЬНЫЙ ОБХОД клеток всё того же квадрата.

Теперь таблица соответствий будет иная.

 

Исходный квадрат Вертикальный обход зигзагом (№№ шагов обхода)	1	2	3	4	5	6	7	8	9
Итоговый квадрат	4	3	8	9	5	1	2	7	6

 

Важно обратить внимание на то, что  лимб – 9 имеет свою оцифровку, которая фактически отображает собой просто-напросто последовательность ШАГОВ ОБХОДА (по какой бы траектория шаги этого обхода не были бы проложены!)

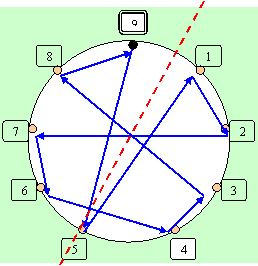
      Сравнивая между собой оба лимба (Рис. 3 и Рис. 4) можно видеть, что результаты отображения у двух разных способов обхода – различны!

       Более красивой и симметричой получилась картинка на лимбе 9 с вертикальным порядком обхода (по столбцам, слева – направо, а по клеткам – сверху – вниз) - Рис. 4.

 

 

 

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 Рис. 4

      Из этих примеров видно, что далеко не любой способ обхода следует выбирать в качестве основного при исследованиях числовых образов разных объектов (в нашем случае – квадратов).

     Информативность и наглядность разных способов – разная и многие важные детали могут ускользнуть от внимания при выборе неэффективного способа отображения.

 

Получив, однако, более красивую картинку, мы должны:

·        Подумать о причинах такого именно результата.

·        Подумать, в чём именно отличие разных способов обхода, дающих разные результаты.

·        Попытаться понять – а что общего имеют цифры (на лимбе и в квадрате), которые после употребления данного способа отображения вдруг оказались по разные (или по одну) стороны оси симметрии.

·        Попытаться понять, почему порядок обхода дуально разделил одни числа (цифры) от других.

КРОМЕ ТОГО!

Задумаемся ещё и над смыслом  рассмотренного выше способа отображения и изучения цифровых (числовых) объектов, использующего лимбы.

1.      С формальной стороны это  - способ подмены цифр в одном квадрате на другие цифры

2.      Способ с применением Лимба, однако, предусматривает любые (сознательно выбранные!) траектории обхода изучаемого объекта, в том числе и такие, которые могут выявлять взаимные связи двух разных объектов. Например, связь цифр в магическом квадрате с цифрами, описывающими траекторию фигуры И-ЦЗЫН

3.      Картинка на лимбе - 9 отображает собой скрытый (не очевидный, невидимый, скрытый) процесс трансформации исходной системы цифр в новую систему. В новую итоговую систему цифр, где алгоритм (правило) преобразования задаётся Исследователем.

4.      Правило трансформации (преобразования) логично назвать «оператором» преобразования, (или алгоритмом преобразования).

5.      В отличие от других ОПЕРАТОРОВ  ПРЕОБРАЗОВАНИЯ процедура отображения на лимбе – 9 приспособлена, прежде всего, для наглядного изучения числовых, арифметических объектов, где набор элементов сводится, обычно, к первым 9-ти цифрам

6.      В данном способе существует возможность не только трансформировать данные одного цифрового объекта в данные другого объекта в соответствии с нужным исследователю ОПЕРАТОРОМ, но и модифицировать форму отображения результатов трансформации, взяв, например, ЛИМБЫ с другим числом точек по окружности (Лимб – 5, Лимб -3, Лимб – 6  и т.д.).

7.      Результаты обработки цифровых объектов и систем СПОСОБОМ ЛИМБОВ, по сути, являются графически наглядными ОБРАЗАМИ изучаемых цифровых объектов. И образы эти, зачастую, гораздо более информативны, чем традиционные способы отображения цифровых объектов и систем в виде таблиц, квадратов, простых графиков и т.п.

8.      Использование СПОСОБА ЛИМБОВ показывает, что с их  помощью проще выявляются, например, циклические закономерности коды, описывающие исследуемый объект.

9.      «Лимбические» картинки – графики наиболее интересных цифровых объектов и систем, вроде магических квадратов, часто можно встретить там, где их наличие никак нельзя было бы даже заподозрить. Выявление таким способом общих механизмов и закономерностей – одно из преимуществ данного метода. Т. о. данный способ, как инструмент, способен к выявлению ОБЩИХ закономерностей, свойственных совершенно разнородным (по физической сути) явлениям (системам)

10.  Имея перед собой ЛИМБИЧЕСКИЙ ОБРАЗ цифрового объекта (системы), можно преобразовать этот образ, например в привычную декартовую систему координат, с помощью которой затем мы получим возможность увидеть график временнго или «псевдовременного» процесса развития изучаемого объекта.

11.  Весьма удобна и эффективна также обратная процедура, когда имея описание процесса (в декартовых координатах) мы можем трансформировать этот график в ЛИМБИЧЕСКИЙ ОБРАЗ, а потом исследовать последний, применяя к нему  разные ОПЕРАТОРЫ ПРЕОБРАЗОВАНИЯ. А затем снова отобразить результаты в любую другую систему координат (например, в виде квадратов и таблиц).

12.  ЛИМБИЧЕСКИЙ СПОСОБ позволяет не только выявлять и анализировать цифровой объект (систему) и процессы в них, но и конструировать более гармоничные, симметричные, сбалансированные цифровые модели объектов, устраняя при этом возможные ошибки и недоработки в согласии с Законами гармонии Природы.

 

Рассмотрим некоторые примеры использования СПОСОБА ЛИМБОВ в изучении цифровых систем.

 

На рисунке Рис.5 (см. ниже) представлена картина классического Круга китайских триграмм, расположенных по окружности.

Согласно данным одного из самых глубоких исследователей китайской философии – А.И. КОБОЗЕВА (см. «Учение о символах и числах в китайской классической философии») Круг системы Учения Книги перемен -  И-ЦЗЫН был в разных религиозных направлениях не одинаковым.

 

Показанный ниже Круг (Рис.5), только он (!), спустя десятилетия споров и дискуссий стал в китайской философии основополагающим и классическим.

 

Внутри данного Круга, (по способу лимбов) был построен графический образ с триграммами этого Круга, как элементами цифрового объекта.

Этот графический образ представляет собой траекторию последовательного обхода позиций триграмм (в сущности – цифр), расположенных на Круге, в порядке возрастания их числовых значений, соответствующих каждой триграмме.

 

Необычную, красивую и гармонично сбалансированную фигуру мы можем видеть в виде траектории линий (красным цветом в центре Круга на рисунке 5).

 

Мы видим, что лимбический способ выявил ранее скрытую от глаза гармонию «чисел – триграмм» и, совершенно не случайным образом, связал  их расположение  на окружности Круга И-ЦЗЫН.

 

Не вдаваясь в подробности этой неслучайности, попробуем провести такой же анализ относительно иных вариантов изображения Круга И-ЦЗЫН, использовавшимся в учениях других направлений китайской философии.

 

              Рис. 5

Ниже представлены взятые из книги А. И. КОБОЗЕВА иные трактовки Круга И-ЦЗЫН где был проведён соответствующий лимбический анализ (см. Рис 6, 7, 8).

 

 

 

 

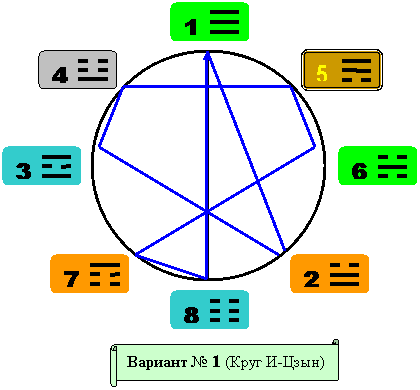
Рис. 6

 

 

  

 

 

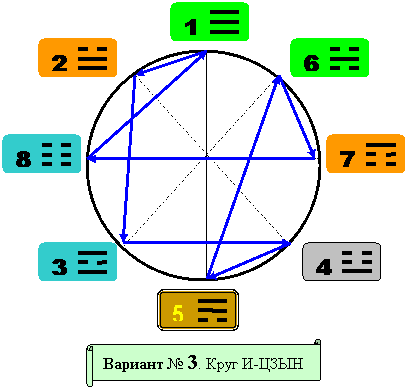
Рис 7

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

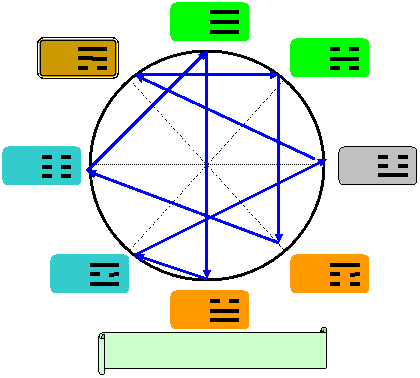
Рис. 8

 

Анализируя вид лимбов на Кругах с фигурами И-ЦЗЫН, (все три варианта иных изображений Круга  И-ЦЗЫН), совершенно не трудно понять - почему самое первое (см. Рис. 5) изображение стало классическим.

 

И, в силу вскрытых обстоятельств, было бы интересно узнать, а почему иные направления китайской философии претерпели угасание и есть ли в этом деле влияние  НЕПРАВИЛЬНО РАССТАВЛЕННЫХ ПО КРУГУ  И-ЦЗЫН триграмм (цифр)?!

 

К сожалению,  в данной статье мы это рассмотреть не можем, так как наша задача иная  –продемонстрировать возможности СПОСОБА ЛИМБОВ по  вскрытию скрытых  пружин цифровых систем и явлений.

В нашем примере была только продемонстрирована возможная цифровая Первопричина неудач существовавших ряда направлений в китайской философии, исповедовавших разные формы представления Круга Книги Перемен (И-ЦЗЫНА), разумеется с позиций моих представлений.

 

То отображение Круга И-ЦЗЫН, которое имеет более гармоничную форму и выявлено  здесь (Рис 5) я буду далее использовать в качестве образца и аргумента в своих исследованиях

 

Что касается «неудачных» форм отображения Круга И-ЦЗЫН, то я, конечно же, не ведаю о конкретных причинах угасания упомянутых выше философских течений. Одно могу, вслед за Пифагором, сказать с уверенностью:  всё так или иначе сводится,  конечном счёте, ТОЛЬКО  к цифрам и к системам цифр.

 

И именно это мне и хотелось лишний раз продемонстрировать, утверждая таким способом правоту  теорий и представлений Великого Пифагора.

 

Некрасивые самолёты – не летают!

Не гармоничные цифровые системы – не живут и не работают!

Москва, 1997г.