А.А.
КОРНЕЕВ
ИССЛЕДОВАНИЕ ПРОЦЕДУРЫ ОКОНЕШНИКОВА
(ПОК)
Результаты предыдущих исследований
процедуры ПОК
http://kaa-07.narod.ru/CHISLO/NewUmn.html
- Во-первых, с помощью Метода Лимбов
нетрудно увидеть, что каждый из 9 «контейнеров» Большой таблица – малые
таблички (3х3) это ничто иное, как развёрнутые КОДЫ саморепликации
соответствующих (по месту в Большой таблице) Первоцифр
- Второе, что мы можем сказать, это
то, что и в большой и в малых таблицах обход ячеек осуществляется «методом
змейки» (слево – направо и снизу – вверх).
- Однако, результат умножения зависит от того, с какого контейнера мы начали умножение, то есть от того - каков
будет МНОЖИТЕЛЬ, ибо внутренняя
организация цифр
(чисел) внутри каждого из контейнеров соответствует индивидуальной структуре
внутреннего движения саморепликации
соответствующей Первоцифры (см. лимбы каждого из контейнеров). А они – различны
(и по направлению движения, и по характеру, и по частоте).
- Это означает, что конечный
результат умножения существенно определяется МНОЖИТЕЛЕМ (у нас – цифрой
«5»), его особенностями и свойствами,
так как все дальнейшие процедуры действия не
меняются.
- МНОЖИМОЕ же задаёт своими цифрами
(каждая в своём разряде!) по сути дела ТРАЕКТОРИЮ ОБХОДА малой таблички, то
есть является по сути дела – КОДОМ ОБХОДА малых квадратов (контейнеров).
- Этот КОД СЧИТЫВАНИЯ формирует тот
самый набор ЧИСЕЛ, из которого далее будет получен искомый
результат.

Цифра 5 имеет
собственный код: 516273849, а код множимого, напомню = 15647.
Сравнив коды, видим,
что совпадает только одна связь, да и та отличается своим противоположным
направлением!
Код считывания малой
таблички (множимое) =
15647.
Согласно авторскому
методу, результат умножения есть следствие процедуры сложения и выписывания
(справа – налево) цифр Старшего разряда последнего числа с Младшим разрядом
предыдущего Числа;
При этом крайние цифры
остаются без изменения.
Будем манипулировать,
как говорилось ранее, сслева – направо.
Тогда , результат будет
такой:
5 (3+0) (2+0) (3+5)
(2+5) – 532870. А теперь отразим данное число в зеркале – 078235!

В
чём же смысл «хитрой процедуры»?
Несмотря
на разное содержание контейнеров-ячеек множителей и одинаковые (в наших
примерах) коды обхода Множимого, Множители организованы по сходной схеме и по
одному алгоритму.
Стало быть, в центр внимания
отчётливо «вплывает» эта «хитрая процедура»
попарного сложения чисел элемента траектории, когда (по ходу
траектории) слагают цифры чисел по правилу: М+С (младший разряд 1-го числа со
Старшим разрядом 2-го числа) или по правилу С+М, когда мы ведём счёт с другой
стороны.
Индексация по
правилу Оконешникова
А теперь
попробуем использовать указанную процедуру для индексации собственно связей
траектории на лимбе и проанализируем такой лимб.
Действуем по
ходу траектории и пользуемся, значит, правилом – «М+С», откуда получаем такие
индексы для элементов абриса (траектории), которые соответствуют результату
умножения.
|
Элемент
|
1) |
1-5 |
5-6 |
6-4 |
4-7 |
(2 |
|
Правило
М+С |
0 |
(6+3)
= 9 |
(0+3)=3 |
(6+2)=8 |
(4+4)=8 |
2 |
|
Результат: |
0 |
9 |
3 |
8 |
8 |
2 |
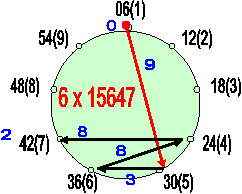
Из
картинки выше можно сделать ещё ряд обобщений:
- Если некий лимб цифруенся (к
примеру, по часовой стрелке) цифрами натурального ряда.
- Если рядом с этими цифрами
проставляют (в порядке следования) числа развёрнутого кода одной из
Первоцифр.
- Если затем, используя цифры
первичной, натуральной оцифровки, на лимб наносят произвольную траекторию
(отражающую некое
число)
- И если осуществляют «хитрую
процедуру» сложения разных разрядов попарных цифр элементов траекторми с
выпистой таких сумм и добавлением крайних цифр (правило М+С, по ходу
траектории)
- То тогда – всё проделанное – НОВЫЙ
ВИД (способ) умножения НЕКОЕГО ЧИСЛА на заданную ПЕРВОЦИФРУ.



ЧАСТЬ 2
Даьнейщее исследование
ПОК
|
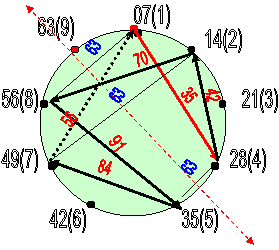
Сумма элементов абриса:
35+42+70+91+84+56 = 378
На этом лимбе произведена
оцифровка под то, чтобы лимб СТАЛ МНОЖИТЕЛЕМ = 7
Траектория на Лимбе,
которая соответствует числу
(1/7 х
10+7) =
1428571
Значит, обход по узлам
оцифровки абриса (с дальнейшим обсчётом) будет умножением
1428571 х 7 =
9999997.
Проверим с помощью правила
Оконешникова:
07-28-14-56-35-49-07
Установим скобки: 0(7-2)
(8-1) (4-5) (6-3) (5-4) (9-0)7
Произведём сложение в скобках и
получим число: 09999997 – 9999997
===================================================================
Сумма элементов абриса Эннеаграммы: 35+42+70+91+84+56 =
378
Для хохмы проведём процедуру Оконешникова с этим рядом:
3 (5+4) (2+7) (0+9) (1+8)
(4+5) 6 --- 3999996!
3999996 = 7х 571428 =
(74 х1666 – 70) = (75 х238 – 70) = (76 х34 –
70)
3999996 : 378 = 10582 = 2х11х13х37
3999996 = 7х (4/7) х 107 = (74 х1665 + 2331) = (75 х238 – 70) = (76 х34 – 70)
3999996 = 4 х 107 = (74 х1665 +7х9х37) = (75 х238 – 70) = (76 х34 – 70)
9999997 : 3999996 = 2,5 = 2 (1/2)
ЭВРИКА!
Если это подтвердится для другой
траектории, то это будет весьма значительно!
Изменим траекторию
(произвольно!); Опять возьмём магический квадрат с кодом обхода змейкой –
438951276

Сначала выполним УМНОЖЕНИЕ
ПО-ОКОНЕШНИКОВУ:
Пункты траектории: 28-21-56-63-35-07-14-49-42-
Расставим скобки по правилу Оконешникова:
2) (8-2) (1-5) (6-6) (3-3) (5-0) (7-1) (4-4) (9-4) (2
Результат умножения = 3072658932
–307,2659х107
КОНТРОЛЬ: 438951276 х 7 ~ 3072658900 – по
калькулятору!
Все
ПРАВИЛЬНО!
Теперь в ШУТКУ:
- Сумма элементов траектории:
(28+21) – (21+56)- (56+63)-(63+35)-(35+07)-(07+14)-(14+49)-(49+42) –(42+28)—Замкнул фигуру в цикл!
- Складываем скобки
(49) – (77)- (119)-(98)-(42)-(21)-(63)-(91)- (70)
- Оставляем числа:
49– 77-119-98-42-21-63-91- 70
- Ставим новые скобки:
4) (9– 7) (7 –11) (9-9) (8-4) (2-2) (1-6) (3-9) (1-7) (0
- Суммируем скобки
4) (9– 7) (7 –11) (9-9) (8-4) (2-2) (1-6) (3-9) (1-7) (0
5 (7) (9) (9) (2) (4) (8) (2) (8) (0
5) (7) (9) (9) (2) (4) (8) (2) (8) (0 --- 5799248280
Результат сложения сумм отрезков (по процедуре) =
579924821 – 57,992 х
108
- Проверка идеи:
307,2659х107 : 579,92
х 107 = 0,5298 – НЕУДАЧА! Должно быть 2,5!
ОПЫТ
2.
Попробуем более простое
число –
147.
Умножим число 147 на число 7 на калькуляторе: 147
х 7 = 1029
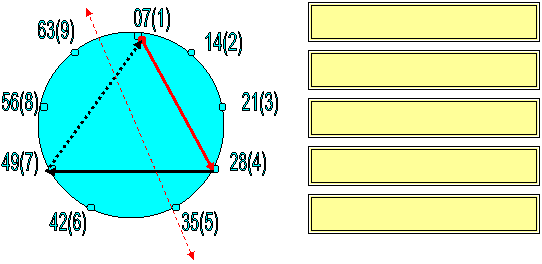
Пропишем путь
траектории:
07-28-49
0) (7-2) (8-4) (9
Получаем число: 1029 (смотрим 2
варианта)
- 07-28-49-07 (Замкнуто) или же 07-28-49 (Не замкнуто!)
- 0) (7-2) (8-4) (9-0)7 /Замкнуто/ или же 0) (7-2) (8-4) (9. /Не замкнуто!/
- 10297 (Замкнуто) или же 1029. /Не замкнуто!/
1029 - ПРАВИЛЬНО!
«ДОПОЛНИТЕЛЬНЫЕ
РАСЧЁТЫ»;
- Сумма элементов по пути обхода – (07+28) – (28+49) – (49+07)
(07+28) + (28+49) + (49+07) = 35-77-56 = 168 =(3 х 7 х 8) = 24 х 7
- Делаем новые скобки для набора чисел 35-77-56 --- 3) (5-7) (7-5) (6 == 4326
- Получаем число: 4326 = 2х3х7х103 = 6х7 х 103 = 42 х 103
РАЗНЫЕ
ФОРМУЛЫ:
- 168 = 3х7х8 = 24х7
- 4326: 168 = 25,75 = 103 : 4
- 4326 = 103 х 42
- 4326: 1029 = 4,2040816 = 206 : 49 =
(103 х 2) : 49 = (103
х 2) : (7х7)
- 4326:7 = 618 = 6 х 103
- 1029 = 147 х
7
- 1029 : 168 = 6,125 = 49 : 8 = (7 х 7) : 8
- 1029:168 =(147х7): (21х8) = 147: (3х8) = (21х7): (3х8) = 49:8
- 618 : 168 = 3,6785714 = 103: 28 = 103 : (4х7)
- 1029 :
618 = 1,6650485 = 343:206 = 343 :
(2х103) = (7х49) : (2х103)
- 75
= 16807; 74 =
2401; 73 = 343; 72 = 49;
- 1029
= 2401 : (7/3) = (2401 х 3) : 7 = (74 х 3) : 7
Выявились константы
– 103*, 49,
7*
- 103
:7 = 14,714286 =
(0,1471286 х 700):7
- 103 х 7 = 721
- 103 х 49 = 5047

ВЫВОДЫ:
- Абрис числа должен быть НЕ ЗАМКНУТЫЙ!
- Лимб, должен быть саморепликационный (для любого числа!)
Опять возьмём магический квадрат с кодом обхода змейкой –
438951276
Таблица
А
|
2 |
7 |
6 |
|
Конец.
Верхний
ярус (Множитель 100) |
|
9 |
5 |
1 |
Середина.
Средний
ярус (Множитель 103) | |
|
4 |
3 |
8 |
Начало.
Нижний
ярус (Множитель 106) |
Попробуем
представить код (число) магического квадрата таким
способом:
438951276 = (438 х 106)
+ (951
х 103)
+ (276 х 100)
=
Последовательность прядка действий
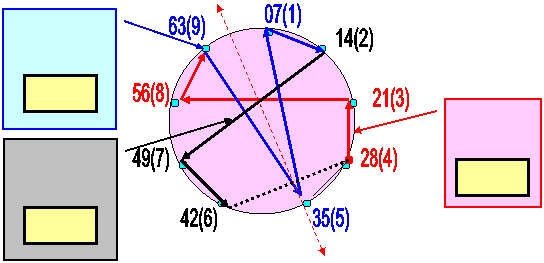
- Делаем саморепликационный Лимб-9 на число «7»: [7.14.21.28.35.42.49.56.63]
- Вводим двойную оцифровку: [07(1). 14(2)…..56(8). 63(9)]
- На лимбе рисуем траекторию магического квадрата, считывая числа этого квадрата (по правилу «змейки»).
- Действуем в ПРАВИЛЬНОМ направлении – змейкой (снизу слева – направо вверх) по ярусам
- Обход строго по направлению стрелок!
- Выписываем узловые точки-числа траектории
- Формируем наборы чисел
- Наборы чисел подвергаем процедуре «ПОК»
- Помним ярус +. Множитель 10х (кроме множителя = 7) со своей степенью «х»
- Ярусные результаты складываем, как простые числа
- Итог – есть результат умножения Магического Квадрата на число «7»
Итак, применим процедуру
«ПОК» (по ярусам магического Квадрата – см. Таблицу
А):
·
Верхний ярус -
276 à 14-49-42
à 1) (4-4)
(9-4) (2 à 1932 =
276 х 7; NU(1932) = 6
·
Средний ярус -
951 à 63-35-07 à 6) (3-3)
(5-0)7 à 6657 = 951 х 7; NU(6657) =
6
·
Нижний ярус -
438 à 28-21-56
à 2) (8-2)
(1-5) (6
à 3066 = 438 х 7; NU(3066) =
6
Общая сумма результатов
ПОК:
- 3066 + 6657 + 1932 = 11655;
- 11655 = 7 х (438+951+276); NU(11655) = 6
Итоговая
формула:
438951276 = (438 х 106) + (951 х
103) + (276 х 100) =
438951276 = (3066 х 106) + (6657 х 103) + (1932 х 100)
=

Вывод: Значит, обход по стрелке + ХИТРАЯ ПРОЦЕДУРА (ПОК) означают:
- Результат в НИЖНЕМ ЯРУСЕ (438) есть умножение на 7 И УМНОЖЕНИЕ РЕЗУЛЬТАТА «ПОК» на 106, то есть – (438 х 7)х106
- Результат в СРЕДНЕМ ЯРУСЕ (951) есть умножение на 7 И УМНОЖЕНИЕ РЕЗУЛЬТАТА «ПОК» на 103 ,то есть – (951 х 7)х103
- Результат в ВЕРХНЕМ ЯРУСЕ (276) есть умножение на 7 И УМНОЖЕНИЕ РЕЗУЛЬТАТА «ПОК» на 100 , то есть – (276 х 7)х100
ОПЫТ 3
Код абриса «БАБОЧКА» на лимбе: 124875
Представим
себе, что мы проверяем умножение этого абриса на число
7:
Должен получиться результат:12487 х 7 =
874125
Исходный код Множимого представляем, как 124х103 + 875х100
Мы должны будем получить 7 х 124 х103 + 7 х 875 х100 = 868х103 + 6125х100
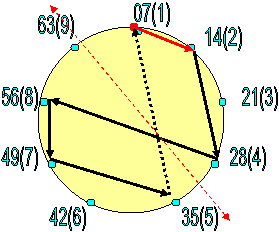
Осуществим обход абриса, в котором НЕИЗВЕСТНО КОЛИЧЕСТВО ЯРУСОВ?
Попробуем разделить обход на 2 части (т.к. 6 знаков числа
можно разделить на 1 ярус /где 3 ячейки!/ и получить 2 таких яруса) и
проведём ПОК:
- 07-14-28 --- 0) (7-1) (4-2) (8 --- 868 (!) Всё правильно!
и
·
56-49-35
--- 5) (6-4) (9-3) (5 --- 6125 (!) Всё
правильно!
А если осуществить ПОК для всей траектории
разом?
07-14-28-56-49-35 --- 0) (7-1) (4-2) (8-5) (6-4) (9-3) (5 -- 874125; Всё правильно!
Так как: 124875 х 7 = 874125
(!)

А что новое знание даёт в
отношении НЕИЗВЕСТНЫХ АБРИСОВ?
КАК УЗНАТЬ – ЧТО ОНИ
ТАКОЕ?
Прежде всего, вполне очевидно, что на лимбе размерности = 1 любой неизвестный абрис отображается 1 в 1, т.е. сам по себе. Значит, лимб-9 должен быть оцифрован именно в этой размерности.
Проведём дополнительное
элементное исследование полученного только что
лимба.
Код абриса «БАБОЧКА» на лимбе: 124875
Выполним процедуру ПОК для элементов абриса «Бабочка»
124875 х 7 = 874125

![]()
![]()
![]()
![]()
![]()
Для всей фигуры «новое умножение» даст величину:
07-14-28-56-49-35
-- 0) (7-1) (4 –2) (8-5)
(6-4) (9-3) 5 -- 874125
874125 : 7 = 124875
Из процедур умножения вскрывается, открывается, простая логика собственной оцифровки элементов абриса
- 07-14 --
0 (7-1) 4 ==
84 = 12х7, но 07-14 = 07(1) –
14(2) -- 12
- 14-28* -- 1 (4-2) 8 == 168 = 24х7, а 14(2)-23(4) дают 24
- 28-56 -- 2 (8-5) 6 == 336 = 48х7
- 56-49* -- 5 (6-4) 9 == 609 = 87х7
- 49-35 -- 4 (9-3) 5 == 525 = 75х7
- 07-35 – 0 (7-3) 5 == 105 = 15х7
- 56-07 -- 5 (6-0) 7 == 567 = 81х7
- 49-14 -- 4 (9-1) 4 == 504 = 72х7
- 42-21 -- 4 (2-2) 1 == 441 = 63х7
- 35-56 -- 3 (5-5) 6 == 406 = 58х7
- 28-07 -- 2 (8-0) 7 == 287 = 41х7
- 35-14 -- 3 (5-1) 4 == 364 = 52х7
- 28-49 -- 2 (8-4) 9 == 329 = 47х7
ОТСЮДА!
Собственный «ВЕС» абриса (сумма всех чисел его оцифровки): 12+24+48+87+75
= 246
НО,
конечного результата такая оцифровка элементов, увы, не обеспечивает!? Почему???
При умножении на 7 абрис получаем – 246 х 7 = 1722 ВСЕГО_ТО!??
Попробуем
сложить числа соответствующие элементам абриса:
84+168+336+609+525 = 1722. Нет!
ПАРАДОКС – процедура ПОК для всей
траектории верна, а по элементам – НЕТ!
При этом в предыдущем случае, когда траектория делилась на две части (по 3 элемента) и производилось дополнительное умножение на 103 и 100 результат получался - правильный!
В этом опыте такого не делалось!
Значит, надо попробовать опять вернуться к степеням, но детализировать упомянутые 2 части.
Итак, в предыдущем случае мы
делали так:
Мы делили обход на 2 части, т.к. 6 знаков кода числа можно
разделить на 1 ярус, /где 3 ячейки!/ и получить 2 таких яруса/ и проводить
ПОК:
- 07-14-28 --- 0) (7-1) (4-2) (8 --- 868 (!) Всё правильно!
и
·
56-49-35
--- 5) (6-4) (9-3) (5 --- 6125 (!) Всё
правильно!
А при осуществлении ПОК для
всей траектории разом мы имели:
07-14-28-56-49-35 --- 0) (7-1) (4-2) (8-5) (6-4) (9-3) (5 -- 874125; Всё правильно!
И где тут наши элементы траектории?
Вот они: 07-14-28-56-49-35
Однако заметим, что тут нет ОТДЕЛЬНЫХ элементов 14-28; и 56-49;, а вот ярусы по 3 узла – ЕСТЬ!
Кстати – число ярусов не полное (не 3 яруса), а только 2 яруса, но в данном случае это не повлияло на результаты, ибо мы здесь учли также и возведение в нужную степень чисел каждого яруса.
Может быть, и при поэлементном умножении (отображении) надо каким-то образом поступать также? Но как это сделать?
Как мы делали в предыдущем
случае:
- ….Мы имели код абриса «БАБОЧКА» (множимого) на лимбе: 124
875…..
- ….Этот исходный код
«Бабочки» мы представили как
124х103 + 875х100
- и тогда получалось, что 7 х 124 х103 + 7 х 875
х100 = 868х103 + 6125х100…
- …. Конечный результат мы представляли в РАЗМЕРНОСТИ
Множимого!!!
- …А числа 868 и 6125 мы уже получали «новым
умножением», из процедуры ПОК, применяя её к цепочкам: 07-14-28 и 56-49-35 соответственно….
Значит, деление на 3 элемента
(на ярусы!) для получения правильных результатов обязательно, даже если из не 3
штуки, а только 2.
А, если мы умножаем с помощью
прямой процедуры Оконешникова НЕКОЕ (любое) число, состоящее из произвольного
числа цифр, то тогда такие «тонкости»
(со степенями!) ни к чему… Умножение производится по принципу «в целом»….
Забавно!
Ну, так что же всё-таки происходит с
элементами?
Как происходит умножение отдельных
элементов?
ЭВРИКА!
А что, если множимое (число 124 875)
представить так:
1х105+2х104+4х103+8х102+7х101+5х100
Тогда, исходя из поэлементной
оцифровки, (см. ниже) имеем:
·
07-14 -- 0 (7-1) 4 == 84 = 12х7, - первый элемент абриса
·
14-28* -- 1 (4-2) 8 == 168 = 24х7, - второй элемент абриса
·
28-56 -- 2 (8-5) 6 ==
336 = 48х7- третий элемент абриса
·
56-49* -- 5 (6-4) 9 == 609 = 87х7- четвёртый элемент абриса
·
49-35 -- 4 (9-3) 5 ==
525 = 75х7- пятый элемент абриса
А где ШЕСТОЙ?
Ведь у нас в формуле
(см. выше) – 6 элементов! Где же тогда у нас этот Последний элемент траектории,
который не меняется в процедуре ПОК?
Для данного случая это – замыкающий абрис элемент, который не надо было
учитывать, так как из-за этого
дублировался Первый узел.
Попробуем посчитать пока без
него…
Напомню себе (и читателю), мы должны получить такой результат «нового умножения»:
07-14-28-56-49-35
--- 0) (7-1) (4-2) (8-5)
(6-4) (9-3) (5 -- 874125;
Итак, сделаем замену в
формуле, подставляя в неё данные процедур ПОК, осуществлённых над единичными
элементами.
84х105+168х104+336х103+609х102+525х101+5х100
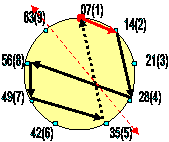
8 400 000
+ 1 680
000
+ 336
000
+ 60
900
+
5 250
+
?
-----------------------
= 10 482 15(?)
Нет! НЕ ВЫХОДИТ!
Но может быть дело в степенях? Попробуем варианты, чтобы понять… Нет! ОПЯТЬ НЕ
ВЫХОДИТ!
Тогда,…
вспомним, что:
…. Конечный
результат мы представляли В РАЗМЕРНОСТИ
Множимого!!!
Множимое у нас - 124 875. ОЖИДАЕМЫЙ РЕЗУЛЬТАТ – 124875х7 =
874125
Ещё одна попытка, сгруппируем
данные парами – всего пар будет 3!
Значит: 124 875 = 12х104 + 48х102 +
75х100
[07-14]; [28-56]; [49-35];
Тогда попарное преобразование по ПОК даст нам всего три числа:
07-14
--- 0) (7-1) (4 --- 84
28-56
--- 2) (8-5) (6 --- 336
49-35 -- 4) (9-3) (5 --- 525
Тогда: 84х104 +
336х102 + 525х100
= 840000+ 33600+525 =
874125 (!) ПОЛУЧИЛОСЬ!
Значит, нужно внести в правила такой
пункт:


Теперь мы снова возвращаемся к исходному вопросу, к
центральному вопросу:
А что это новое знание даёт в
отношении
НЕИЗВЕСТНЫХ
АБРИСОВ?
КАК УЗНАТЬ – ЧТО ОНИ ТАКОЕ,
АБРИСЫ?
КАК ВЫРАЖАТЬ ИХ ЧИСЛОМ В
ЦЕЛОМ?
Всё-таки, так или иначе, с
группировками или в целом, но у нас получился свой вариант применения процедуры
Оконешникова (хитрая процедура - «ПОК») для того, чтобы производить умножение
любых чисел, представляемых графическими абрисами, новым способом и
непосредственно на лимбах.
Мы смогли полуэмпирическим
методом сформулировать Правила для «ПОК» и приблизиться к решению главного
вопроса – научиться выражать фигуры (на лимбах) ЧИСЛОМ.
|
Следуя заветам Великого
Пифагора, мы уяснили для себя (и, возможно, для читающих), что ...красота
(абрисов) не содержит в себе ничего, кроме ПРОПОРЦИЙ... А пропорции – не
содержат в себе ничего, кроме … ЧИСЛА. Между тем, даже у
красивых абрисов – МНОГО пропорций, а значит – МНОГО
чисел… |
А как же быть с идеей выражения
фигуры (вещи) только ОДНИМ числом?
·
Надо ли для этого сводить множество пропорций к
одной?
·
Или надо считать приближением к цели, выявляемые
путём числовых анализов часто повторяющиеся числа-константы?
Во всяком случае, мы выработали
интересный метод числового анализа, который, в рамках Метода лимбов, с помощью
которого уже были получены многие интересные результаты, позволит лучше уяснить
и суть этих результатов и двинуться дальше.
Что нам тут «светит»?
Во-первых, теперь стало ясно
существенное и специфическое влияние (на все результаты) и применение
репликационных оцифровок Лимбов.
Во-вторых, стало понятно, что
процедура ПОК имеет право на жизнь и для применения (апробации
исследования) на лимбах с
ИНОЙ оцифровкой
В – третьих, выявилась важность
ярусной организации чисел оцифровки, По крайней мере, стала понятна причастность
такой организации к Пифагоровской таблице умножения.
Игра с оцифровками лимба,
применение РАЗНЫХ видов и Правил обхода баз исходных данных (например, квадратов
3х3), содержит как множество
возможностей, так и множество неясностей.
|
В настоящее время, по крайней мере, мне, неизвестны
НИКАКИЕ экзотерические способы анализа процессов взаимодействия абрисов
фигур с оцифрованными (так или иначе!) лимбами. |
А нам нужны именно такие
методы.
Что ж – будем двигаться в этом
направлении. А данный материал на этом закончим
А.А.
КОРНЕЕВ
Москва, 22 августа